| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 유니티서바이벌게임만들기
- unity3dservival
- 백준
- Unity
- 유니티3dui
- c#코테
- unity3d게임만들기
- c#기본문법
- 유니티공부
- c#
- 백준 구현문제
- 백준 C++
- unity게임
- 백준코테
- c#기초문법
- 백준코딩테스트
- 유니티게임만들기
- 유니티
- c#코딩기초트레이닝
- 티스토리챌린지
- c#문제
- c#프로그래머스기초문법
- 백준 c++ 공부
- unity3d
- 바킹독
- unity게임만들기
- 오블완
- c# c#프로그래머스
- C#문법
- 바킹독알고리즘
- Today
- Total
나 개발자 진짜 되냐?
백준 C++ 1977번 완전제곱수 ( sqrt(a), ceil(x) ) 본문

오늘은 알고리즘 고수를 영접했다.
내가 백준을 보며 이런 티어가 존재하나? 의 급의 사람이었다.
나에게 solved 문제를 class별로 풀어보라고 조언해 주셨다.
오늘까지 풀고! 다음으로 넘어가야겠다 ㅎ
감사합니다 ༼ つ ◕_◕ ༽つ

오늘은 완전제곱수!
최근에 어떤 문제를 풀면서 누적곱에 대해 기억해서
약간 그런 제곱수를 찾는데에 괜찮지 않을까? 하며 작성했다.
애초에 10000개 이하니까
글자는 총 100개 밖에 안될 것이다.
그래서 벡터에 일단 완전제곱수를 저장해 놓고?
범위에 들어오면 꺼내는 식으로 진행하려고 했다.

흠
근데 테스트케이스는 맞는데 답이 틀리단다..
흠.. 어디가 문제지?
제씨를 찾았다.
내 정답률은 90 퍼라고 했다.
그래서 나머지 10 퍼로 힌트를 달라고도 안 했는데 또 cout에서 오류라고 알려주었다.
그렇다 m의 경우 글자를 내야 하는데 ' ' 이건 띄어쓰기 즉 char형이어서 문제가 된다는 것이다.
그래서 일단 if / else로 작성했다
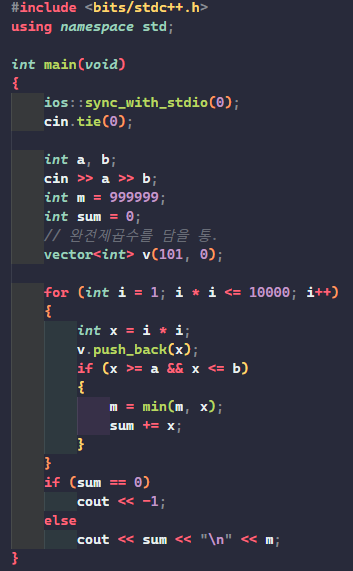
이랬더니! 성공!!!
그럼 어떻게 삼향연산자로 cout을 쓸 수 있을까? 했다.
( sum == 0 )? ( cout << -1 ) : ( cout << sum << "\n" << m);
해주면 된다고 한다.

그냥 cout안에서 하는 게 아니라 밖에다가 괄호만 열면 가능하다는 사실을 알았다!
그렇다면 최적의 풀이는 무엇일까?!
이것도 괜찮다고 하지만 또 다른 아이디어가 있다며 제안해 주었다.
sqrt(a)
a의 제곱근을 구하는 식이다.
근데 제곱근이라고 해서 딱! 떨어지는 것이 아니라
막 3.333 이런 것도 있으니까
이런 것을 반올림, 올림, 버림 해주는 친구 세 친구가 있다.
ceil(x) - 올림
floor(x) - 내림
round(x) - 반올림
x가 만약에 3.14라면
ceil(x) = 4
floor(x) = 3
round(x) = 3
이 된다.
이 x에 sqrt(a)를 넣어주면
이 식을 반올림, 버림, 올림 해주겠다는 뜻이 된다.
for문 자체에 넣어주면 계산이 한결 쉬워진다.
for문 안에는 이미 a부터 b까지의 범위이니
a랑 가장 가까운 친구가 최솟값이 되어서
굳이 min안 써도 첫 번째에 넣어주면 된다!
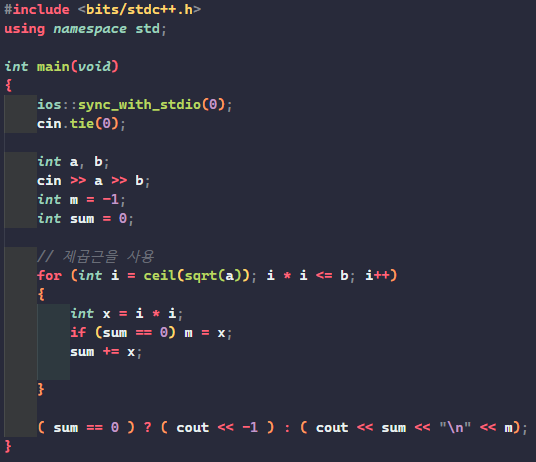
이러면 vector도 필요 없고 min 도 안 써도 되고,
근데 생각보다 어려운 거 같기도 하고?
m 값에도 아무거나 들어가도 될듯하다.
오늘은 내 생각을 바탕으로 거의 다 맞은! 문제였다.
나 정말 실력이 는 걸까!!!
'C++을 시작해봐요! > 구현문제를 알아보아요!' 카테고리의 다른 글
| 백준 C++ 2920번 음계 ( if문 두번쓰기 ) (1) | 2026.02.03 |
|---|---|
| 백준 C++ 25501번 재귀의 귀재 ( s.length, string_view ) (1) | 2026.02.02 |
| 백준 C++ 1550번 16진수 ( 누적곱, stoi, hex ) (0) | 2026.01.29 |
| 백준 C++ 9093번 단어 뒤집기 ( getline, stringstream ) (1) | 2026.01.28 |
| 백준 C++ 1292번 쉽게 푸는 문제 ( 누적합 ) (1) | 2026.01.27 |





