| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- unity3d
- 백준 구현문제
- 백준코테
- c#코테
- C#문법
- c# c#프로그래머스
- 백준 c++ 공부
- 오블완
- c#코딩기초트레이닝
- Unity
- 유니티3dui
- 유니티게임만들기
- unity게임만들기
- 바킹독알고리즘
- 유니티서바이벌게임만들기
- 백준 C++
- unity3d게임만들기
- c#기본문법
- 백준코딩테스트
- c#
- 티스토리챌린지
- c#기초문법
- 유니티
- 백준
- 바킹독
- c#프로그래머스기초문법
- 유니티공부
- unity3dservival
- unity게임
- c#문제
- Today
- Total
나 개발자 진짜 되냐?
백준 C++ 15829번 Hashing ( mod M, 시그마란? ) 본문

이번 주는 참 춥다.
수면바지도 찾아 입었다.
추운 게 싫긴 한데...
가끔 나는 온난화로 지구가 점점 따뜻해진다고 하던데.. 하며
더 추워지면 지구가 덜 아프려나? 하는 생각에
이런 추위를 견딜 때가 있다.

내가 정말... 이 문제의.. 이 함수를... 어.. 알아야 할까?

... r은 31, M은 뭐 1234567891....
음음
그리고 다행히? 친절하게? 힌트를 주었다.
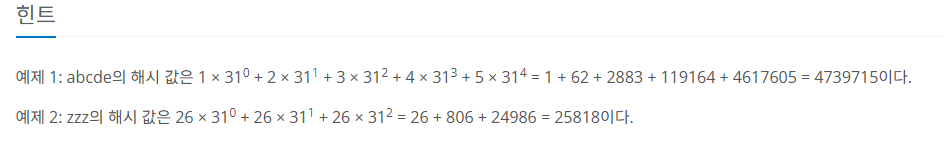
위에 힌트 두 개는 5줄 3줄일 때인데.. 문제는 50줄인 경우도 풀어야 해서.. 그게 문제다
최대
그럼 뭐 31의 50승까지 알아야 하는 상황..
어휴 어제는 7의 635승도 하고
정말 머리가 터지기 직전이다.
일단.. 5개짜리라도 해볼까?
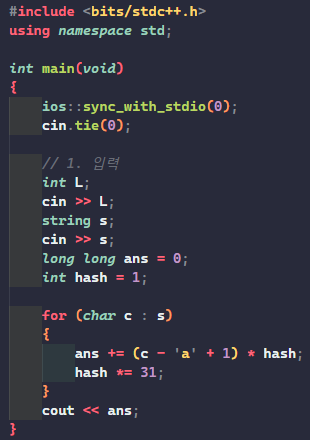
답은 잘 나온다.. 이제 50개짜리를 풀어야 하는데..
도대체 어떻게 풀 수 있을까?
지금 드는 생각은 저 M을.. 어찌 활용해야 할 거 같은데..
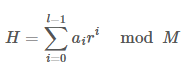
식에서 보면 이게
ai랑 mod M 해주어야 하고
ri랑도 mod M을 해주어야 한다.
여기서 mod는 나누기이다. 늘 쓰던 % 이 친구
흠 그렇다면.. 원래 내식에서 사용이 가능할까?
도전해 봤다.

그냥 M을 나누기해 주었는데도
5개짜리의 답이 아까와 같다...??
오...
작은 데이터 일 땐 나눠봤자 몫일테니 상관없는 거였다.
마치 5를 8로 나누면 나머지가 5인 거처럼 말이다!
시그마에 대해 내가 헷갈리는 거 같아서 정리할 겸 가져왔다.

아까식을 가져와서

시그마 기준으로
위에 있는 L-1 // 밑에 있는 i=0
이거는 컴퓨터로 표현하면
for ( int i = 0; i < L; i++ )이다.
ai는 s [i] - a + 1; 즉 a 한 글자 가져와라
내 식에서는 c - 'a' +1 이 되겠다.
r의 i승은
뭐 hash를 i승 곱한 값이 되겠다.
내 식에서는 hash *= 31; 이 되겠다.
근데 우리는 여기서 mod M이 옆에 있어서 M을 나눠줘야 하니까
(ai * ri) % M인 셈이고
사실은 그렇게 따지면 ai랑 ri를 곱해주고 M을 나눠주면 편한데?라고생각하겠지만
그러면 수가 너무 커져버려서
분배법칙으로 먼저 값을 깎은 다음에
곱해주게 되는 것이다.
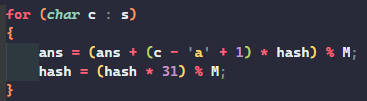
답은 어찌 됐든 같으니까 말이다!

크크크 백점!

내가 생각했던 식이랑 비슷해서 놀랐고?!
두 번째는 시그마를 더 확실히 알아가는 거 같아서 좋았다.
결국 사실문제에 답이 다 있었는데 말이다..ㅋㅋㅎ
내일의 나, 이 문제를 풀 수 있을 것인가!!!
'C++을 시작해봐요! > 구현문제를 풀어봤어요!' 카테고리의 다른 글
| 백준 C++ 17478번 재귀함수가 뭔가요? ( 재귀함수 ) (3) | 2026.01.23 |
|---|---|
| 백준 C++ 1032번 명령 프롬프트( fill ) (2) | 2026.01.22 |
| 백준 C++ 1009번 분산처리 ( 일의자리 구하는 법 ) (1) | 2026.01.20 |
| 백준 C++ 9506번 약수들의 합 ( 제곱근, 완전수 ) (2) | 2026.01.19 |
| 백준 C++ 11005번 진법 변환 2 ( reverse, 몫과 나머지 ) (0) | 2026.01.16 |





