| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 유니티게임만들기
- 백준코딩테스트
- c#코딩기초트레이닝
- c#문제
- 오블완
- 바킹독
- 티스토리챌린지
- 바킹독알고리즘
- 유니티공부
- unity3d
- c#기초문법
- 백준 C++
- c#
- unity게임
- c# c#프로그래머스
- C#문법
- unity3d게임만들기
- 유니티3dui
- Unity
- c#코테
- 유니티서바이벌게임만들기
- 백준 구현문제
- 백준코테
- c#기본문법
- 백준 c++ 공부
- 백준
- unity게임만들기
- 유니티
- unity3dservival
- c#프로그래머스기초문법
- Today
- Total
나 개발자 진짜 되냐?
백준 C++ 2745번 진법 변환 ( 진수는 누적 곱! ) 본문

나는 Mr.mine이라는 게임을 즐겨한다.

방금 찍은 사진인데.. 천시간이 넘었네...
ㅋㅋㅋㅋ 사실 방치형 광산게임이다 보니까..
아직... 한참 멀었다.
2566km가 끝인데
나는 이제 1586km이다.
1km를 파는 데 걸리는 시간은..

... 뭐 사실 게임을 켜두면 가끔 빨리 파지는 버프를 받을 수 있긴 한데..
오프라인으로 내버려둔다면 85시간 뒤에 1km를 파는 셈이다.
ㅋㅋㅋㅋㅋㅋ그러니 천시간이 넘어버렸네.
이렇게 파기만 해도 되나? 싶어서
I 임에도.. 정보를 얻기 위해 들어가게 된 디스코드 커뮤니티..
한국사람들은 별로 없지만.. 외국인들이 꽤 활발하게 대화가 오고 가고 있었다.
나 같은 사람이 이렇게 많다니... 하며 ㅋㅋ 감탄했다.
어제는 게임을 플레이하며 아무리 해도 안 나오는 유물 때문에
나오는 게 맞는 건가???? 싶어서 그 커뮤니티에 처음으로 채팅을 남겼다.
어떤 분이 유물은 실존한다고 해주셨고 ㅋㅋ
그거에 대한 꿀팁도 주셨다.
감사하다고 말씀드리고.. 이분은 어떻게 이렇게 잘 아는 걸까? 하며 디스코드를 보는데
꽤 고위직?이라고 해야 할까
일반인이 아니었다. 개발자 같았다.
켜놓은지 200시간 됐다고 적혀있었다. 개발자인가 보다.. 근데 아직 이게임을 개발하고 계신 건가? 싶기도 하고..
기분이 굉장히... 뭐랄까 벅찼달까??
나도 나중에 어느 한 게임의 개발자가 되어
누군가에게 이런 꿀팁을 주는 사람이 될 수 있을까.. 하며
마음을 크게 부풀리기도 했다.
ㅋㅋㅋㅋ썰이 꽤 기네...

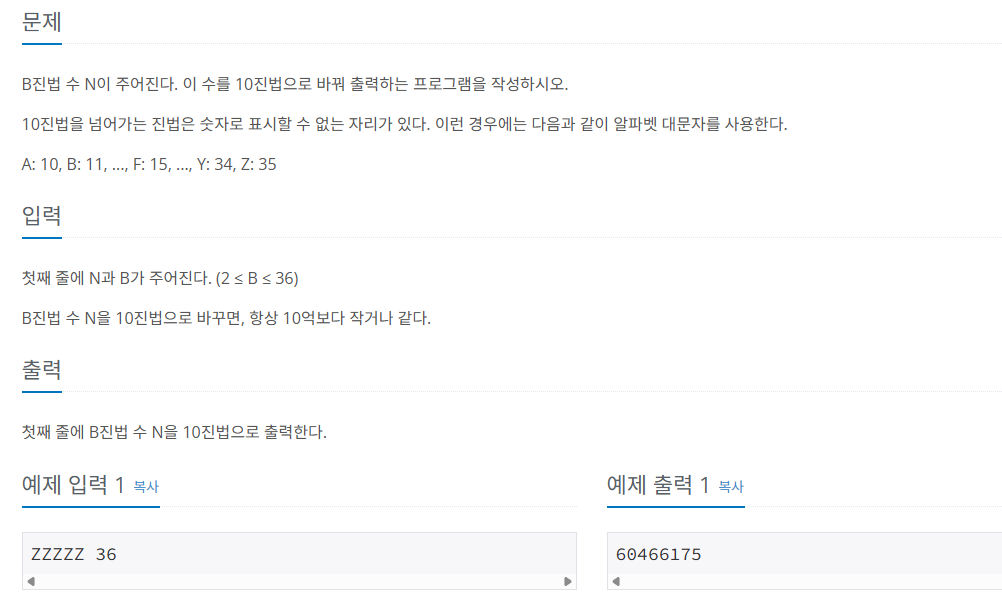
B진법수...?
뭐지.. z는 35인데.. 36진수가 있다는 건가?
일단 10억 정도라고 알려주었으니 int인건 알겠는데
진짜 이건 푸는 것도 푸는 건데 진짜 문제를 이해하는 게 저어어엉말 힘든 거 같다.
일단 어떠한 진법을 10진법으로 바꾸라는거 같은데..
지 선생에게 물어보았다.
10진법은
0부터 9까지 표현 가능하다.
그니까 B 진법, 여기서는 36까지 된다고 하니까..
36진수는
0부터 35까지 표현이 가능하다는 뜻이 된다.
228이라는 숫자를 10진법으로 한다면
2 * 100 + 2 * 10 + 8 * 1
이렇게 각 자릿수마다 0이 추가되는 모습.
그래서 ZZ를 36진수 하게 된다면
z는 35니까
35 * 36 + 35 * 1 = 1295가 된다.
ZZZZZ 36이라면
35 * 36^4 + 35 * 36^3 + 35 * 36^2+ 35 * 36 + 35 * 1
가 되는 것이다.
흠....
일단 36까지 알려주며 Z를 설명해 주는 거 보니..
문자열로 접근해야 할 거가 같고..
이다음이 문제인데
A는 10, B는 11... Z는 35를 어떻게 다 하나하나 적겠는가..
그리고 결국 문자열로 하나씩 다 잘라야 하는데..
for로 잘라도 되려나..? 헷갈린다.
결국 지 선생에게 물어봤는데.....
1. 0부터 9까지 들어오는 경우가 있고, A부터 Z까지 인경우를 두 가지로 나눠서 생각해야 한다.

그래서 나누어주었다.
나누어주고
문자열이니까 숫자로 표시하기 위해서는
'0'을 해줘야 하고
문자열도 결국 숫자로 더해주기 때문에
'A'를 해줘야 한다
그리고 A의 시작은 10이기 때문에
글자에서 A 빼주고 더하기 10 해줘야 한다.
여기서 특이했던 문제 방식이 있다.
123의 경우
왼쪽의 숫자가 가장 큰 자릿수인데..
이 문제를 풀려면 맨 왼쪽부터 풀어야 하는데
몇 글자인지 모르면 풀 수가 없다는 것이었다.
근데 지피티가 새로운 시각을 알려주었다.
1을 하고 *10 하고 +2 하고 또 *10 하고 +3 하면 답이 같다는 사실이다!!
으잉? 이게 무슨...??
기존 값을 키우면서 더하는 방식으로 하면
거듭제곱을 외울 필요도 없다는 것이다.
1A2F 16
인경우
0 * 16 + 1 = 1
1 * 16 + 10 = 26
26 * 16 + 2 = 418
418 * 16 + 15 = 6695
반대로
1 * 16^3 + 10 * 16^2 + 2 * 16 + 15 * 1
= 6695
가 나오게 된다.
아니 어떻게 이게 가능한 거지..?!
뭐 분배법칙 덕분이라고 한다.
누적 곱 방식이라고도 하며
저 위에 식을 그대로 가져와서 쓰면
(((0*16 + 1)*16 + 10)*16 + 2)*16 + 15
인 거고 이것을 분배법칙으로 나누면
1*16^3 + 10*16^2 + 2*16^1 + 15*16^0
이렇게 된다는 것이다.
그래서
이 식을 그대로 쓰면
ans * n + ( c-'0')
혹은
ans * n + (c-'A'+10) 이 된다.

흠..... 여기서 내가 헷갈렸던 이유를? 생각해 보면
처음에 지 선생은 나에게 이렇게 설명해주지 않아서였던 거 같기도 하다.
처음에는 나에게
고정적으로 곱해주는 값이 있고, 더해주라고 했었어서..
뭘 곱해주라는 건지 뭘 더하라는 건지 정말 도통 몰랐었다....

미리 곱하기를 해주어서
다음에는 그냥 더하기만 해주는 방식이다.
아까보다 식은 더 간단한데
해석하기엔 훨씬 어려웠다.
그래서 조금? 더 쉬운 방법을 알려달라 해서 위의 식을 알게 되었다.
사실 오늘 날짜로 지 선생의 프로생활은 끝났다.
무료버전이라 그런지...설명을 이해하는데 조금 어려워졌다......
ㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋㅋ....
스읍 미안하다.
그래도
확실한 건
몇 진수의 값을 구할 땐
각 자릿수에 따라 ^5 ^4 이렇게 해줄 필요 없이
이렇게 누적 곱을 해주면 된다는 사실을 알게 되었다.
신기하다.
신기하다.
또 내가 몰랐던 수학 공식을 하나 알았다.
재밌다.
아니 안 재밌다.
하나도 안 재밌다.
이래서 내가 코테 문제 풀겠냐고오오오오오
빼애애액
'C++을 시작해봐요! > 구현문제를 풀어봤어요!' 카테고리의 다른 글
| 백준 C++ 11723번 집합 ( 비트마스크 ) (0) | 2026.01.14 |
|---|---|
| 백준 C++ 2747번 피보나치 수 ( 배열 ) (0) | 2026.01.13 |
| 백준 C++ 25206번 너의 평점은 ( mapping, 실수 출력 형식 ) (1) | 2026.01.09 |
| 백준 C++ 1924번 2007년 ( switch, 배열 출력 ) (0) | 2026.01.06 |
| 백준 C++ 7568번 덩치 ( 브루트포스, vector<pair> ) (0) | 2026.01.05 |





